The vibrant ecosystem of community-produced learning content
Today Martin Weller wrote that, while the open source movement is a wildly successful model for producing software, we “haven’t really cracked a community based production model for learning content”. David Wiley followed up to say that, given our lack of progress in this area since the 90’s, he believes there’s “a good argument to be made that a community based production model for learning content isn’t actually possible.
Do better work
I want you to do better work.
I joke that my hobby is talking people out of going to law school. It’s a joke because it gets a chuckle, but it’s not really a joke because I do actually take every chance I get to talk people out of going to law school.
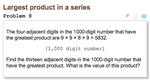
Project Euler Problem 8: Largest Product in a Series
When I first learned to program I didn’t explore too much. I played it safe. I took things I knew how to do and I applied those to each new problem I found, no matter how well suited the solution actually was to the problem.
The Bitterness Trap
I got my start in computing early because my dad was disabled. He had a degenerative nerve disease and at some point, maybe when I was five or six, my clumsy little kid hands got better at wrangling computer parts than his own traitorous hands.
The Hand Raiser Problem and Inequality
While I was at Thinkful our instructional design and features evolved a lot. At the beginning things were simple. The curriculum was plain text (a Google doc we shared) that curated 3rd-party resources and “explained” (in a way that will make instructional designers cringe) the remaining topics.
Project Euler Problem 7: 10001st prime
Back to primes! So far we’ve been able to get away with being a little greedy with our compute when playing with primes. Now Euler is ratcheting up the difficulty and we’ll have to focus on efficiency.
Project Euler Problem 6: Sum Square Difference
Problem 6 has a brute force solution and an elegant formula solution that calculates the answer directly. But the brute force solution is good enough and the formula is obscure enough that I wouldn’t have found it without googling so we’ll focus on the brute force solution.
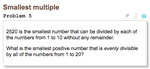
Project Euler Problem 5: Smallest Multiple
Problem 5 is a lot of fun (well, “fun”) because (1) there’s a very simple program requiring no math that calculates the answer, but (2) that program would need impossible amounts of compute to actually run, and (3) you can figure the answer with pen and paper super fast if you think about the math a bit.
Project Euler Problem 4: Largest palindrome product
Project Euler problem 4 feels like a step back in difficulty. The numbers involved aren’t too big so we don’t have to worry about resource constraints. The subproblems it breaks down into are fairly straightforward.
Project Euler Problem 3: Largest Prime Factor
Problem 3 is where Euler starts forcing us to consider resource limitations. Before, the most straightforward solution worked just fine, even if it used more resources than a less complex algorithm would.